بحث عن المصفوفات

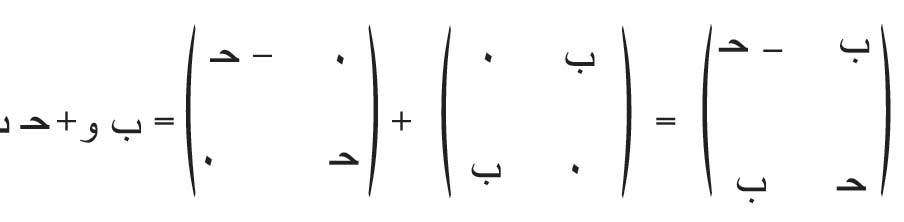
المصفوفة هي مجموعة من الأشكال المستطيلة المكونة من مجموعة من الأرقام أو الرموز أو العبارات، والتي تسمى أيضًا بالإدخالات أو العناصر، وجميعها منتظمة ومرتبة في صفوف وأعمدة، وتنقسم المصفوفة إلى قسمين، الأولى هي المصفوفة الحقيقية، والثانية هي المصفوفة المعقدة.

تنقسم شكل المصفوفة إلى خطوط أفقية وعمودية، وتتضمن عناصرها الأعداد الحقيقية والأعداد المركبة، ولها تاريخ طويل في حل المعادلات الخطية، وكانت تسمى سابقًا باسم “صفائف” منذ ظهورها في عام 1800 م، وانتشر استخدامها في دول الصين وأوروبا وجميع دول العالم عن طريق العلماء .

تم ابتكار مصطلح المصفوفة لأول مرة في عام 1848 من قبل جي. جي. سيلفستر، كاسم لمجموعة منتظمة ومرتبة من الأرقام. وفي عام 1855، قدم أرثر كايلي المصفوفة كتمثيل لعناصر خطية، وهذه الفترة اعتبرت بداية الجبر الخطي ونظرية المصفوفات ودراسة فضاء المتجهات في المجال المحدد، وهو فرع من الجبر الخطي. يساهم هذا الفرع في نظرية التشفير ويؤدي بشكل طبيعي إلى دراسة واستخدام المصفوفات في المجال المحدد في نظرية التشفير. والوحدة هي تعميم لفضاء المتجهات ومن الممكن اعتباره فضاء المتجهات على حلقة، وهذا يؤدي إلى دراسة المصفوفات حول الحلقة. ونظرية المصفوفات في هذه المنطقة لا تعتبر فرعا من الجبر الخطي. يمكنكم الحصول على مزيد من التفاصيل في الموسوعة .

بحث عن المصفوفات بالعناصر

تُعَدُّ المصفوفات حاليًا واحدةً من الاستخدامات الرياضية المستخدمة في مختلف أنواع البرمجة الحاسوبية والذكاء الاصطناعي، والتي تمكن الآلات والحواسيب من اتخاذ القرارات التلقائية. وسنتحدث في هذا البحث عن المصفوفات وسنحدد بعض العناصر للحديث عنها كما يلي:

حجم المصفوفة

يتم تحديد حجم المصفوفة بناءً على عدد الصفوف والأعمدة التي تحتويها. يتم رمز المصفوفة عادة بـ (م ن)، ويشير رمز (و م × ن) أو (م ن- by) إلى عدد الأعمدة. يشار إلى أبعاد المصفوفة بـ (م و ن). وتسمى المصفوفة التي تحتوي على صف واحد بناقل الترتيب، والتي تحتوي على عمود واحد بناقل العود. تسمى المصفوفة التي لها نفس عدد الصفوف والأعمدة بالمصفوفة المربعة، والتي ليس لها عدد محدد من الصفوف والأعمدة بالمصفوفة غير المحددة، بينما تسمى المصفوفة التي لا يوجد بها صفوف أو أعمدة بالمصفوفة الفارغة.

حساب المصفوفة

يمكن أن تنسب حسابات المصفوفات إلى تقنيات متنوعة ومختلفة في كثير من الأحيان، حيث تتمتع بالقدرة والإمكانية لحل العديد من المشكلات باستخدام طريقتين: الخوارزميات المباشرة والنهج المتكرر. على سبيل المثال، يمكن استخدام المتجهات الذاتية للمصفوفة المربعة للعثور على تسلسل للنقالات (الذي تم ذكره سابقا) عندما تقترب من المتجه الذاتي وتصبح قيم صفوفها لا محدودة. ومن المهم أن تتمكن من اختيار خوارزمية مناسبة لحل مشكلة محددة، لذا يجب تحديد فعالية ودقة جميع الخوارزميات المسموحة والمتاحة. يطلق على دراسة هذه المسائل العددية في الجبر الخطي مصطلح نطاق، وهي مثال للعديد من الحالات العددية الأخرى. فكل حالة لها جانبين أساسيين ورئيسيين، وهما: تعقيد الخوارزميات والاستقرار العددي. لتحديد تعقيد الخوارزمية، يجب وجود حدود علوية أو تقديرات لعدد العمليات الأولية مثل الجمع والضرب.

التطبيقات على المصفوفة

تتواجد الكثير من الاستخدامات للمصفوفات سواء في مجال الرياضيات أو في مجالات أخرى، حيث يمكن استخدامها للفائدة والاستفادة منها من خلال تمثيل مضغوط لمجموعة من الأرقام في المصفوفة، وذلك باستخدام مجموعة من البدائل لأي عملية تحتاج إلى حسابات معقدة. وتوجد لها العديد من النظريات المهمة، ومن بينها الاحتمالات والإحصاء (والتي تطبق على المصفوفات العشوائية) والمربعات (والتي تستخدم ناقلات الاحتمالات وتتطلب إدخالات غير قابلة للسلبية) والتماثلات والتحويلات، والتي تلعب دورًا أساسيًا ورئيسيًا في الفيزياء الحديثة، خاصة في مجال الجسيمات والرسم البياني والتحليل والهندسة والتركيبات الخطية والإلكترونيات والبصريات الهندسية.

خصائص المصفوفات

يتم تسمية كل عنصر في المصفوفة بأنه عنصر المصفوفة، سواء كان هذا العنصر رقمًا أو رمزًا أو قيمة جبرية، وتتميز المصفوفات بعدة خصائص منها:

• تُعبّر العناصر التي توجد داخل المصفوفات عن طريق كتابة الحرف الذي يُعبّر عن اسم المصفوفة، وكتابة رقم الصف والعمود الخاص بالعنصر على الترتيب تحت ذلك الحرف؛ أي اسم المصفوفة صف، عمود
• إذا كان عدد صفوف وأعمدة إحدى المصفوفات متساويًا لعدد صفوف وأعمدة مصفوفة أخرى، فإن هاتين المصفوفتين تعتبران متساويتين في الحجم
• يمكن تسمية المصفوفة باسم تبدأ به أي حرف من حروف اللغة العربية، وفي اللغة الإنجليزية يتم تعبير عنها باستخدام أحد الحروف الكبيرة

ويتم توضيح كل تلك الخصائص الخاصة بالمصفوفات من المثال التالي: [+6+4+24] [+1-9+8] ونلاحظ التالي:

• ب3،1: يشير إلى العنصر الذي يقع في الصف الأول والعمود الثالث ويساوي 24
• ب1،1: يعني العنصر الذي يوجد في الصف الأول والعمود الأول ويساوي 6
• ب3،2: تعني العنصر الذي يقع في الصف الثاني والعمود الثالث ويساوي 8

أنواع المصفوفات

توجد الكثير من أنواع المصفوفات، والتي من بينها كل مما لي:

• مصفوفة الوحدة Identity Matrix
• المصفوفة المربعة Square Matrix
• المصفوفة المتعامدة Orthogonal Matrix
• المصفوفة المفردة Singular Matrix
• المصفوفة المثلثية العليا Upper Triangular Matrix
• المصفوفة القطرية Diagonal Matrix
• المصفوفة المثلثية السفلى Lower Triangular Matrix
• المصفوفة المتساوية Equal Matrix
• المصفوفة القياسية Scalar Matrix
• المصفوفة الصفرية Null Matrix
• مصفوفة العمود الواحد Column Vector
• مصفوفة الصف الواحد Row Vector
• المصفوفة الهرميتية Hermitian Matrix
• المصفوفة المستطيلة Rectangular Matrix
• المصفوفة المتماثلة Symmetric Matrix
• المصفوفة غير مفردة Non-Singular Matrix

محدد المصفوفة

يتم استخدام محدد المصفوفة في العديد من التطبيقات، بما في ذلك حل نظام من المعادلات الخطية وإيجاد مصفوفة عكسية والعديد من التطبيقات الأخرى في علم الرياضيات، ويتميز محدد المصفوفة بالعديد من المزايا، بما في ذلك ما يلي:

• يمكن العثور عليها فقط إذا كانت المصفوفة مربعة
• يمكن إيجاد معكوس المصفوفة فقط إذا كان محددها ليس يساوي الصفر
• يستخدم الرمز |أ| للإشارة إلى قيمة المصفوفة، ويستخدم نفس الرمز للإشارة إلى القيمة المطلقة؛ على سبيل المثال، يرمز محدد المصفوفة أ بالرمز |أ|
• أنه عدد حقيقي

يمكن العثور على محدد المصفوفة عن طريق استخدام القانون التالي: محدد المصفوفة = أ × (ج × ت – ك × ي) – ب × (د × ز × ي) + ث × (د × ك × ج)، ويستند هذا القانون إلى ضرب كل عنصر في الصف الذي تم اختياره في المصفوفة ذات الأبعاد الثنائية، ويتكون الصف الأول من (أ ب ج) على التوالي، ويمكن الحصول على هذه المصفوفة بعد استثناء العمود والصف الذي يحتوي على العنصر المحدد في الصف الأول.

أسئلة شائعة