بحث عن الدائرة ومحيطها ونظريتها في الرياضيات
يقدم هذا البحث، عزيزي القارئ، معلومات حول الدائرة ومحيطها. فالدائرة هي واحدة من الأشكال الهندسية الأولية، وقد عرفها الإنسان القديم ورسمها على جدران المعابد، واستخدمها في النقوش ورسم قرص الشمس. وفي الهندسة، تشكل الدائرة خطًا منحنيًا بسيطًا ومغلقًا، وكل نقطة في هذا الخط تبعد نفس المسافة عن نقطة الارتكاز، والتي تسمى مركز الدائرة، ويُطلق على المنطقة داخل الدائرة اسم القرص .
والدائرة في الهندسة الأقليدية تعرف على أنها مجموعة غير منتهية من النقاط الواقعة في مستوى والتي تبعد نفس البعد عن نقطة ما وهي المركز كما تسمى أي نقطة من على المحيط إلى المركز بنصف القطر ولمعرفة المزيد عن الدائرة وخصائصها عليكم بالبقاء معنا في موسوعة .
تعريف الدائرة ومحيطها
تتميز الدائرة بأنها من الأشكال الهندسية المميزة التي تختلف عن المثلث والمربع والمستطيل والخماسي والسداسي، حيث تفتقر إلى الأضلاع وتتكون من مجموعة من النقاط التي تدور حول المركز، ويُطلق على هذا الجزء اسم محيط الدائرة .
خصائص الدائرة
- وتر الدائرة : هو أي خط مستقيم يصل بين أي نقطتين على سطح الدائرة، ويعتبر أطول وتر في الدائرة هو الذي يمر بمركزها، وفي حالة مرور الوتر بمركز الدائرة، يُطلق عليه قطر الدائرة، حيث يُسمى كل وتر في الدائرة باسم “قطر .
- قطر الدائرة : يُشير هذا المصطلح إلى أي خط مستقيم يمر من سطح الدائرة إلى الجانب الآخر منها، ويمر عبر مركزها .
- نصف قطر الدائرة : الخط الذي يربط أي نقطة في دائرة بمركزها هو القطر .
- مركز الدائرة : هو النقطة المتوسطة في دائرة، ويكون قياس المسافة منها إلى أي نقطة على سطح الدائرة ثابتًا .
- π هو رمز ذو قيمة ثابتة : يُستخدم عدد (3.14) في جميع الدوائر بغض النظر عن مساحتها ومحيطها
تكمن العلاقة الطردية بين محيط الدائرة ونصف قطرها في أنه مع زيادة نصف قطر الدائرة يزيد محيطها . - المماس : هو الخط الذي يمر عبر نقطة واحدة على محيط الدائرة .
- القاطع : هو خط يمر عبر نقطتين على سطح الدائرة .
- مساحة الدائرة : يتم حساب المساحة من هذه المعادلة (المساحة = π × نق2)
- القطعة الدائرية : هي قسم من الدائرة، ويفصلها عن باقي الأجزاء الدائرية خط قاطع أو وتر .
- القطاع الدائري : هي جزء من دائرة محيطها نصف قطر وقوس.
- إلقوس : القوس هو جزء من محيط الدائرة الذي يمتد من نقطة إلى أخرى، ويمكن قياس طوله باستخدام هذه المعادلة: القوس = الزاوية × نصف قطر الدائرة)
- الزاوية المركزية : هذه الزاوية التي يتم وضع رأسه فيها مركز الدائرة .
- الزاوية المحيطية : تلك الزاوية التي يكون مركزها في محيط الدائرة .
أهمية الدائرة
نظريات خاصة بالدائرة
- إذا قمنا برسم أي عمود من مركز الدائرة إلى سطحها، سيقسمها إلى نصفين متساويين .
- في حالة توازي وتقاطع وترين في دائرة، يحصران قوسين متساويين في المساحة ومتطابقين .
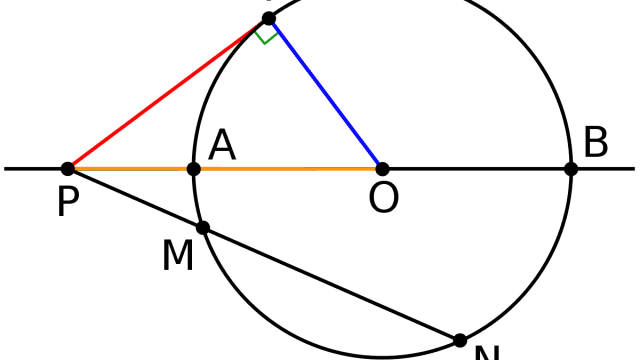
- في حالة مماسين لدائرة من نقطة خارجية معينة، يكون المستقيم الذي يمر بين تلك النقطة ومركز الدائرة عموديًا على الوتر الموجود بين نقطتي المماس.
- عند رسم شكل رباعي داخل دائرة، فإن قياس الزوايا المتقابلة داخل الشكل الرباعي الدائري يكون مجموعها 180 درجة، ويعرف هذا الشكل في الرياضيات والهندسة باسم الشكل الرباعي المحاط بدائرة.