علوم
بحث عن متوازي الاضلاع
توجد أشكال هندسية متنوعة حولنا وتشكل كل الأدوات والمشاهد المحيطة بنا، حيث تكون الشمس دائرية والشباك قد يكون مستطيلًا أو مربعًا، ومن بين هذه الأشكال الهندسية يأتي متوازي الأضلاع الذي سنتحدث عنه في هذه المقالة على موسوعة.
تعريف متوازي الأضلاع:
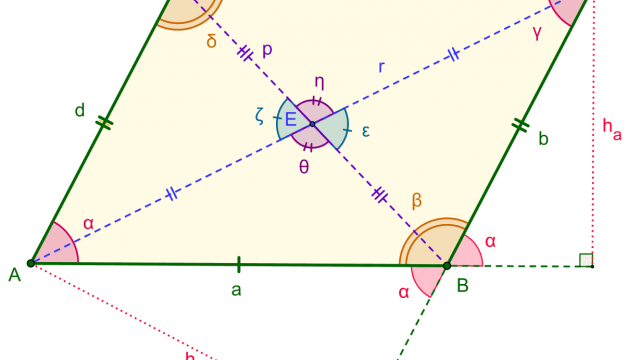
المتوازي الأضلاع هو شكل هندسي رباعي له أربعة أضلاع، وكل ضلعين متقابلين لهما نفس الطول والشكل، أو قد يكونا متوازيين أو متطابقين. وله أربعة زوايا، حيث يبلغ مجموع زواياه 360 درجة كما هو الحال في الأشكال الرباعية الأخرى. وكل زاويتين متقابلتين له لهما نفس القياس، ويتقاطع القطران في المنتصف وينصف كلًا منهما الآخر، ويصل القطر بين الزاويتين المتقابلتين. وكل زاويتين تقعان على نفس الضلع ومجموعهما 180 درجة. يُعرف المتوازي الأضلاع أيضًا باسم “شبيه المعين.
خصائص متوازي الأضلاع:
- تتميز المتوازيات بأن كل ضلعين متقابلين بهما طول متساوٍ ومتطابقٍ.
- يقسم القطران في متوازي الأضلاع القطر إلى نصفين متساويين، حيث يتقاسم كل منهما الجزء الحقيقي من القطر.
- يتميز هذا الشكل بأن الزوايا المتجاورة، أي الناتجة عن تقاطع خطين متوازيين مع خط آخر، تكمل بعضها البعض بزاوية 180 درجة.
- تتساوى زوايا الزاويتين المتقابلتين في درجاتهما.
- تساوي مساحة المتوازي الأضلاع مساحة المثلث الذي يتكون من قطر وضلعين.
- مجموع المربعات المتوازية الأضلاع يساوي مجموع المربعات طولي القطر المتوازي الأضلاع.
- إذا كانت إحدى زوايا متوازي الأضلاع تساوي 90 درجة، أي قائمة، فإن جميع الزوايا ستكون قائمة، لأن كل زاويتين متقابلتين في المتوازي المستطيلي متطابقتين.
- يتقاطع القطران المتوازيان في نقطة واحدة تشكل مركز التناظر له، ويُعرف هذا المركز بمركز المتوازي الأضلاع.
- كل ضلعين من أضلاع متوازية متوازيان.
- إذا مر أي مستقيم في مركز متوازي الأضلاع، فإنه يقسم الشكل إلى نصفين متطابقين.
- إذا توفرت أي من الخصائص السابقة في مضلع محدب رباعي، فإنه يكون متوازي الأضلاع.
حالات خاصة بمتوازي الأضلاع:
- قد يتحول المتوازي الأضلاع إلى شكل هندسي آخر، وهو المعين، إذا تساوت أطوال الأضلاع أو تعامدت، وخاصة إذا كانت الأضلاع المتوازية بجوار بعضها البعض.
- إذا تساوت الأقطار في متوازي الأضلاع، أو أصبحت إحدى زواياه قائمة بزاوية 90 درجة، فإنه يتحول إلى مستطيل.
- يتحول المتوازي الأضلاع إلى مربع عندما تكون زواياه جميعها قائمة، أي تساوي 90 درجة، وتكون أطوال جميع الأضلاع متساوية، وتكون أقطاره متعامدة.
- عندما يتحول المتوازي الأضلاع إلى مستطيل أو معين، يمكن تحويله إلى مربع في هذه الحالة.
محيط متوازي الأضلاع:
- يساوي محيط المستطيل الذي يحيط بأربعة منازل طول أضلاعه الأربعة، وبالتالي يساوي محيط المتوازي الأضلاع طول الضلع الأكبر مضروبًا بـ 2.
- “يُمكن حساب محيط المستطيل عن طريق جمع أطوال الأضلاع الأربعة للمتوازي المستطيل.
- مثال: إذا كان هناك متوازي أضلاع، وكان طول أحد أضلاعه 5 سم وطول الضلع الآخر 6 سم، فإن المحيط يساوي: بما أن أطوال الأضلاع في المتوازي الأضلاع هي 6، 5، 6، 6 سم، فإن محيط المتوازي الأضلاع = مجموع أطوال الأضلاع = 6 + 5 + 6 + 5 = 22 سم
مساحة متوازي الأضلاع:
- يتم حساب مساحة متوازي الأضلاع عن طريق ثلاثة أمور: تحدد الزاوية والقاعدة ومساحة المثلث بشكل محدد.
- وفقًا للقاعدة، مساحة المتوازي الأضلاع = طول القاعدة × طول ارتفاع القاعدة.
- تحسب مساحة المتوازي الأضلاع باستخدام طول أحد الأضلاع وضربه في طول الضلع الثاني المجاور له، ثم ضربه في جيب الزاوية. وجيب الزاوية يعني طول الضلع الذي يقابل تلك الزاوية مقسومًا على الوتر في المثلث القائم الزاوي.
- يمكن حساب مساحة متوازي الأضلاع بضرب مساحة المثلث في العدد 2، حيث يعادل طول قاعدة متوازي الأضلاع طول قاعدة المثلث وارتفاعه يساوي ارتفاع المثلث.
- مثال: إذا كان هناك متوازي أضلاع، وكان طول إحدى الأضلاع 4 سم، وطول الضلع الآخر 5.5 سم، فإن مساحته يمكن حسابها عن طريق قياس الارتفاع الذي يساوي 3 سم، وتطبيق قانون المساحة الذي يتضمن ضرب الارتفاع في طول القاعدة، وبذلك تكون مساحته 12 سم مربع.
التمييز حتى يكون الشكل متوازي أضلاع:
- عندما تتطابق الضلعان المتقابلان في الشكل الهندسي، يصبح المضلع متوازي الأضلاع.
- في حالة قياس زوايا الشكل المتقابلة بمقدار 180 درجة، فإن الشكل يصبح متوازي الأضلاع.
- عندما يتقابل ويتوازى ضلعان في الشكل الهندسي الرباعي فإنه يصبح متوازي الأضلاع.
- عندما تكون الزوايا المقابلة لبعضها متساوية، يتحول الشكل إلى متوازي الأضلاع.
- يساوي قانون المساحة للمتوازي الأضلاع طول الارتفاع مضروبًا في طول القاعدة.
- يكون محيط المستطيل المتوازي الأضلاع مساويًا لمجموع أطوال أضلاعه الأربعة.
- إذا قمت بتقسيم الأطوال في الشكل إلى نصفين، فسيتحول إلى متوازي الأضلاع.
- عند تقسيمه، يتم الحصول على مثلث ومستطيل حين يتساوى طول الأضلاع.