بحث عن المتطابقات المثلثية وأنواعها

•  المثلّث متساوي الساقين.
• المثلّث متساوي الأضلاع.
• المثلّث مختلف الأضلاع.
• المثلّث قائم الزاوية.

(. يتم تقسيم المثلثات إلى عدة أنواع حسب مجموع قياس زواياها، وفقا للتالي:)

• مثلث حاد الزوايا: والذي يتميز بزاوية أقل من 90 درجة.
• مثلث قائم الزوايا: ويتميز بقياس زاوية يبلغ 90 درجة.
• مثلث منفرج الزوايا: ويتميز بزاوية قياسها أكثر من 180 درجة.

تعريف حساب المثلثات Trigonometry

• يندرج حساب المثلثات ضمن فروع الرياضيات، ويهتم بكل ما يتعلق بالمثلثات، مثل حساب المسافات بين الأضلاع وحساب قياس الزوايا. ويعد حساب المثلثات من الأهمية البالغة، حيث يتم استخدامه والاعتماد عليه في فروع كثيرة من العلوم الأخرى، مثل الهندسة والألعاب الإلكترونية وغيرها.
• يتعلق هذا العلم بدوال الزوايا وهي ظل الزاوية وجيب تمام الزاوية وجيب الزاوية.
• يُعد علم حساب المثلثات من بين أشهر العلوم التي اهتمت بها عدة حضارات، مثل الحضارة الصينية والحضارة البابلية والحضارة المصرية القديمة.
• ظهر هذا العلم في شكله الحديث في القرن الثاني قبل الميلاد، عندما قام عالم إغريقي بترتيب جدول القيم المثلثية، ثم وضع علماء هنود قواعد رئيسية له.
• وصلت نظريات علم الرياضيات إلى العالم العربي في العصور الوسطى عندما وضع علماء العرب عددًا من النظريات والقوانين في هذا المجال، وفي القرن السادس عشر، صاغ علماء أوروبا مجموعة من القوانين والنظريات فيه، مما أدى إلى ظهور نظريات جديدة فيه، وكانت أشهرها اللوغاريتمات التي اخترعها جون نابير في عام 1614.

تطابق المثلثات

 يوجد حالات تطابق فيها المثلثات، حيث يتطابق المثلثان إذا كانت أطوال أضلاعهما المتناظرة متساوية، وبالتالي فإن قياسات الزوايا المتناظرة فيهما متساوية أيضًا.

هناك حالات يمكننا من خلالها التعرف على وجود تطابق بين مثلثين، وأحد هذه الحالات هو أن نعلم أن ثلاثة أضلاع من المثلث الأول تطابق الثلاثة أضلاع من المثلث الثاني، وفي هذه الحالة يكون المثلثان متطابقين وزواياهم متطابقة أيضًا.

في حالة معرفة قياس زاوية وطول الضلعين المجاورين لها في كلا المثلثين – حيث تكون الزاوية والأضلاع متساوية في المثلث الآخر – فإن المثلثين متطابقان. وفي الحالة الثالثة، إذا تساوت قياسات زاويتين وضلع واحد في المثلث الأول، وقياسات زاويتين والضلع المتناظر له في المثلث الثاني، فإن المثلثين متطابقان.

تعريف المتطابقات المثلثية

تُعرف المتطابقات المثلثية أو المعادلات المثلثية بأنها متطابقات تتألف من دوال مثلثية. وتُعد هذه المتطابقات مهمة جدًا لأن لها دورًا حاسمًا في حل المعادلات الرياضية وخاصةً في معكوس الدالة.

تتناول المتطابقات المثلثية الثلاثي المكون من ثلاثة أضلاع وثلاث زوايا يبلغ مجموع مقاييسها 180 درجة، وتستخدم هذه المتطابقات في سلاسل الأرقام وعلم الحساب واللوغاريتمات، بالإضافة إلى استخدامها في مختلف فروع الرياضيات.

المتطابقات المثلثية الأساسية

• الظل: رمزه هو (ظا)، ويتم تطبيق قانونه في المثلث القائم الزاوية بالشكل التالي: ظا س = (الضلع المقابل للزاوية س) ÷ (الضلع المجاور للزاوية س) = جا(س) ÷ جتا (س).
• القاطع: رمز المثلث القائم الزاوية هو (قا)، وقانونه هو: قا × س = وتر المثلث ÷ الضلع المجاور للزاوية × س = 1 ÷ جتا × س.
• قاطع التمام: يحمل الرمز (قتا)، ويتبع قانون المثلث القائم الزاوية حيث يكون قتا = وتر المثلث ÷ الضلع المقابل للزاوية، ويمكن كتابته كـ س = 1 ÷ جا س.
• الجيب: ورمزه (جا)، أما عن قانونه في المثلث القائم الزاوية فهو: جاس= الضلع المقابل للزاوية س÷ وتر المثلث.
• جيب التمام: يتم رمز (جتا) في المثلث القائم الزاوية بالقانون: جتا = الضلع المجاور للزاوية س / وتر المثلث.
• ظل التمام: رمز المثلث القائم الزاوية هو (ظتا)، وقانونه هو: ظتا س = الضلع المجاور للزاوية س ÷ الضلع المقابل للزاوية س = 1 ÷ ظا س = جتا (س) / جا (س).

أنواع المتطابقات المثلثية

المتطابقات المثلثية الأساسية تشمل الآتي:

مُتطابقات ناتج القسمة وهي:  

• ظا س = جا س ÷ جتا س.
•  قتا س= جتا س ÷ جا س.

متطابقات الضرب والجمع

• جاس جا ص= ½ [جتا(س-ص)- جتا (س+ص)]
• صيغة جتاس جتا ص يساوي نصف جتا (س-ص) + نصف جتا (س+ص)
• جاس جتا ص= ½ [جا(س+ص)+ جا (س-ص)]
• جتاس جا ص= ½ [جا(س+ص)- جا (س-ص)]

متطابقات الجمع والطرح

• جا (س±ص) = جا (س) جتا (ص) ± جتا (س) جا (ص).
• قاعدة غيتا (س+ص) = غيتا (س) غيتا (ص) – جا (س) جا (ص).
• جتا (س-ص) = جتا (س) جتا (ص) + جا (س) جا (ص).
• ظا (س+ص) = ظا (س) + ظا (ص) / (1 – ظا (س) ظا (ص)).
• ظا (س-ص) = ظا (س) – (ظا (س)/ (1+(ظا س ظا ص)).

 مُتطابقات مَقلوب العدد وتشمل: 

 قتا س= 1÷ جا س. قا س= 1÷ جتا س.

 ظتا س =1÷ ظا س.

 مُتطابقات فيثاغورس و تشمل:

• جتا 2 س+ جا 2 س= 1
•  قا 2 س – ظا 2 س= 1 
• قتا 2 س – ظتا 2 س= 1

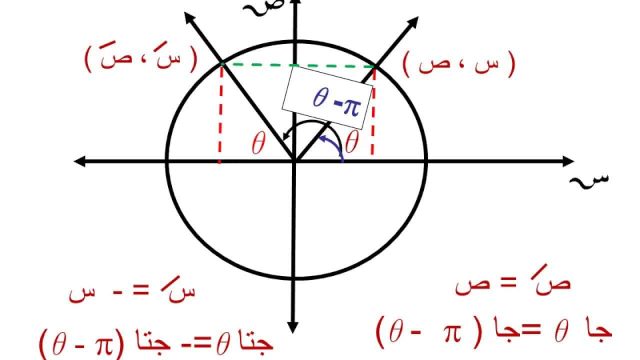
متطابقات الزوايا المتكاملة

• جا س= جا (180-س).
• جتا س= – جتا (180-س).
• ظا س= – ظا (180-س).

متطابقات الزوايا المتتامة

• جا (90-س)= جتا س.
• جتا (90-س)= جا س.
• ظا (90-س)= ظتا س.
• ظتا (90-س)= ظا س.
• قا (90-س)= قتا س.
• قتا (90-س)= قا س.

متطابقات عكس الزاوية

• جا (س/2)=± ((1-جتا س)/2)√
• جتا (س/2)=± ((1+جتا س)/2)√
• ظا (س/2)=± ((1-جتا س)/(1+جتا س))√= جا س/(1+جتا س)= 1-جتا س/ جا س= قتا س – ظتا س.
• ظتا (س/2) = ± ((1+جتا س)/(1-جتا س))√ = جا س/(1-جتا س) = 1+جتا س/جا س = قتا س+ظتا س.

متطابقات ضعف الزاوية وتشمل

• جا 2س= 2 جاس جتاس
• – جتا 2 س= جتا² س- جا² س.
• – ظا 2س = 2 ظاس/ (1-ظا² س)
• – ظتا 2 س=(ظتا²س-1)/2 ظتاس.

 نظرية فيثاغورس

تُعد نظرية فيثاغورث من أشهر النظريات في علم المثلثات، حيث يمكن استخدامها لحساب طول الوتر المقابل للزاوية القائمة في المثلث القائم الزاوية، ويمكن تمثيل قانون فيثاغورث رياضيًا كالتالي: مربع طول الوتر يساوي مجموع مربعي طول الضلعين الآخرين: 

يمكن حساب مساحة المربع عن طريق جمع مربع طول الضلع الأول في المثلث مع مربع طول الضلع الثاني في المثلث.

يعد عكس ما قيل في نظرية فيثاغورث صحيحًا أيضًا، حيث يكون المثلث قائم الزاوية إذا كان لديه مربع ضلع الوتد الأطول يساوي مجموع مربعي ضلعي الوتد الأقصر في المثلث، كما أن قياس الزاوية الخارجية في المثلث يساوي مجموع قياس الزاويتين الداخليتين الأخريتين في المثلث، باستثناء الزاوية المجاورة له.

استخدامات المتطابقات المثلثية في الحياة

بالإضافة إلى استخدام المتطابقات المثلثية في علم الرياضيات وتعليمها في المناهج الدراسية، فهناك العديد من المجالات التي يتم استخدام هذا العلم فيها، ومنها:

علم الفلك

• قبل القرن السادس عشر، استخدم علم الفلك حساب المثلثات لتحديد مواقع النجوم والكواكب، وهو واحد من أول العلوم التي استخدمت هذه الطريقة.
• يستخدم البارالاكس في حساب المسافة بين الكواكب، وبين الأرض والشمس والقمر، وكذلك في حساب نصف قطر الأرض.

العمارة والهندسة

• يستخدم حساب المثلثات في علم الرياضيات أو في علم الهندسة المعمارية لقياس الأعمدة وزوايا جدران المنازل قبل بنائها.
• تعد هذه الخطوة من أهم خطوات البناء التي يجب الانتباه إليها حتى لا تنهار المنازل والأبنية أو تتعرض جدرانها للتشوه.
• بناء أبراج الدعم وتحديد ارتفاعها وقياس المسافة بينها ومعرفة طول الكابلات وتحديد قوة الجسور، كلها تعتمد على علم حساب المثلثات الذي يستخدمه المهندسون.
• تستخدم هذه التقنية خلال عمليات البناء لتحديد الارتفاع المثالي للسلم والمنحدر الذي يتماشى مع السقف، وذلك من خلال استخدام جدار منحني بشكل صحيح.

مجال النجارة

• يستخدم النجارون معرفة حساب المثلثات عند قص الزوايا لمعرفة أبعادها أو تحديد الخطوط المجاورة.

مجال الطيران

• في مجال الطيران، يتم استخدام علم حساب المثلثات لتحديد اتجاه وسرعة الرياح بعد تحديد سرعة الطائرة والرياح.
• من خلال استخدام هذا العلم، يمكن معرفة جانب المثلث الثالث الذي ستتحرك فيه الطائرة على المسار الصحيح.

قياس ارتفاعات المباني

• يستخدم علم المثلثات لحساب ارتفاع الجبال والمباني وتحديد المسافات بينها.

علم الجريمة

• يتم استخدام علم حساب المثلثات بشكل كبير لتحديد مسارات وزوايا القذائف التي يتم إطلاقها في مسارح الجرائم، وهذا من أهم استخداماته.
• يستخدم التقدير في حوادث السيارات لمعرفة أسباب الحوادث والتصادمات.

مجال الملاحة

• يتم استخدام علم المثلثات في مجال الملاحة لتحديد اتجاه وموقع البوصلة والانتقال بين الاتجاهات المختلفة لتحديد المواقع.
• ويستخدم أيضًا في رؤية الأفق وحساب المسافات.

علم الأحياء البحرية

• يستخدم علم حساب المثلثات في علم الأحياء البحرية من خلال استخدام النماذج الرياضية ووظائف المثلثات لمعرفة مدى عمق ضوء الشمس اللازم للطحالب البحرية في عملية البناء الضوئي.
• يستخدم علماء الأحياء البحرية هذا المجال أيضًا لفهم سلوكيات الحيوانات البحرية الكبيرة مثل الحيتان وتقدير حجمها.

الصناعات التحويلية

• تُستخدم العلاقات المثلثية في تحديد أحجام وزوايا الأجزاء الميكانيكية التي تستخدم في صناعة الأدوات والآلات مثل السيارات وغيرها.
• تستخدم شركات السيارات هذا العلم لتحديد أحجام كل أجزاء السيارات بشكل دقيق خلال عملية التصنيع والتحقق من تفاعلها بشكل آمن.
• يستخدم العاملون في مجال الخياطة العلاقات المثلثية الأساسية لتحديد زوايا السهام والتي تساعد في تصميم القمصان والتنانير.

ومن الاستخدامات الأخرى للمتطابقات المثلثية:

• أنظمة الأقمار الصناعية.
• إنشاء الخرائط.
• يُستخدم في علم التفاضل والتكامل.
• يُستخدم لقياس مد المحيطات وارتفاع أمواجها.
• يتم وصف الضوء وموجات الصوت بواسطة الدوال المثلثية الأساسية مثل جيب التمام وجيب الزاوية.
• يتم استخدامه في دراسة ترتيب ذرات الصلب البلوري.
• علم الزلازل.
• التصوير الطبي.
• تطوير اللعبة.
• رسومات الحاسوب.
• نظرية الأعداد.
• الإحصاء.
• الإلكترونيات.
• الصوتيات.
• البصريات.

 

وبهذا نصل إلى نهاية مقالنا عن المثلثات المتطابقة، حيث تم التركيز فيه على تعريف المثلث وحساباته وتطابقه والمتطابقات المثلثية وأنواعها واستخداماتها في الحياة.