بحث عن تمثيل دوال المقلوب بيانيا وخصائصها

يقدم موسوعة بحثًا عن تمثيل الدوال المعكوسة بالرسم البياني، ويعد ذلك درسًا في مادة الرياضيات التي تهدف في المقام الأول إلى تنشيط ذكاء الطالب وتطوير قدراته وتركيزه، وتتضمن هذه المادة دروسًا عن الدوال وخصائصها ومعادلاتها.

يوجد العديد من أنواع الدوال المقلوبة والنسبية والمتغيرة، وفيما يتعلق بتمثيل الدالة بيانياً سوف نعرضه تفصيلاً في المقال التالي.

بحث عن تمثيل دوال المقلوب بيانيا

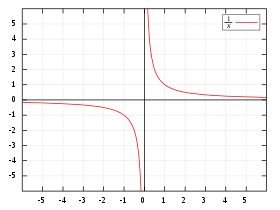
• تعرف الدالة المقلوبة كتلك التي تعكس العنصر (X)، ويمكن شرحها في الصيغة التالية: (f(x)=1/x).
• يمكن توضيح المعادلة التالية (f(x)=[a/(X-b)]+c) بشكل أفضل، حيث تحدد الأرقام المتغيرة a و b و c خطوط الدالة المتقاربة، ومجال ومدى الدالة.
• يتم تمثيل تقاطع الدالة ومحوري الإحداثيات في الرسم البياني للدالة.

خصائص دالة المقلوب

في حال رغبتم في تحديد خصائص دالة المقلوب، يجب تحديد خطوط اقتراب الدالة، ومجال ونطاق الدالة بدقة أكبر، ولتوضيح هذا الأمر بشكل بسيط، سنعرض المثال التالي:

f(x)=2/(X-3)+c، وتكون (a=2, b=3, c=0 ).

المثال بطريقة أخرى:

ص(س)=3/(س-4)، حيث إن أ=3، ب=4، ج=0.

تمثيل الدوال بيانيا

• يمكن تمثيل دالة المقلوب بيانيا باستخدام المعادلة المذكورة أعلاه، ولكن يجب علينا أولا تحديد القيم التي يتكون منها الجدول، والذي يكون فارغا في المرحلة الأولى. ثم يتم تطبيق المعادلة المشار إليها في الجدول باستخدام الرمز (Y)، فعلى سبيل المثال، يتم استبدال قيمة (X=0) في المعادلة التالية (Y=-3/4)، ليتم بعد ذلك تحديد قيم (Y) لجميع القيم (X) ويكتمل الجدول النهائي.
• تشير دالة المقلوب إلى أن قيم (X) التي تجعل المقام يساوي صفر غير معروفة من حيث أصفار المقام.

• وباستخدام هذا الجدول وتطبيق المعادلة عليه، يمكن تحديد خصائص دوال المقلوب.

تحديد مجال دالة المقلوب ومداها

يجب توضيح المقصود من كلا الدالتين أولاً، حتى يتمكن المرء من تحديد مدى ونطاق الدالة:

• المجال: المطلوب هو حل المعادلة التي تحتوي على متغير (x)، وهي كالتالي ({R-{4)، ويشمل ذلك جميع الأرقام الحقيقية باستثناء الصفر والذي يمثله الرقم 4.
• المدى: يتم تحديد قيمة (Y) في المعادلة، كما في ({R-{0)، ونتيجة لذلك، تساوي جميع الأعداد الحقيقية باستثناء القيمة الصفرية لـ (Y) الصفر.

أشكال الدوال المقلوبة

يمكن تقسيم الدوال المقلوبة إلى شكلين؛ دالة الأم ودالة الأبناء، وسوف نوضح ذلك بالتفصيل في الفقرات التالية:

دالة الأم

• الشكل العام لها هو f(x)=1/x.
• تكون الأشياء ثابتة داخلها، ويكون نقطة التماثل فيها تساوي صفر.
• يتساوى مدى الدالة ومجالها بالصفر.
• يكون خط التقارب الأفقي ممثلاً بالمعادلة (Y=0)، وخط التماثل الرأسي ممثلاً بالمعادلة (X=0).

دالة الأبناء

• يتم من خلاله تحديد شكل واتجاه المنحنى.
• تتسع الدالة رأسياً في الحالة التي تكون قيمة الدالة فيها أكثر من (1)، و العكس كذلك إذ تتقلص رأسياً عندما تقل القيمة عن (1).
• لا يتغير شكل الدالة عندما يتم تحديد قيمتها باستخدام الأعداد الحقيقية، ويمكن تمثيل الدالة بشكل عام عن طريق المعادلة f(x) = a/x – h + k، حيث تمثل نقطتا التماثل (h،k) المحاور التي يتقاطعان فيهما خطوط الانحدار، ويكون نطاق الدالة (h)، ومداها (k) وخط التقارب الأفقي (Y=k)، وخط التقارب الرأسي (X=h).

فيما يتعلق بإحداثيات التقاطع مع محوري الإحداثيات، يحدث أحيانًا أن يتقاطع منحنى الدالة مع محور الإحداثيات (X) ولكن يتجنب قطع محور الإحداثيات (Y).